Золотий перетин
Створюю і просуваю комерційні сайти та інтернет-магазини з 2008 року. 27-07-2013, 22:59 26 555 1Ціле завжди складається з частин, частини різної величини знаходяться в певному відношенні один до одного і до цілого.
Принцип золотого перетину - вищий прояв структурного і функціонального досконалості цілого і його частин у мистецтві, науці, техніці і природі.
Золотий перетин - гармонійна пропорція
У математиці пропорцією (лат. proportio) називають рівність двох відносин: a: b = c: d.
Відрізок прямої АВ можна розділити на дві частини такими способами:
- на дві рівні частини - АВ: АС = АВ: ВС;
- на дві нерівні частини в будь-якому відношенні (такі частини пропорції не утворюють);
- таким чином, коли АВ: АС = АС: ВС.
Дивтись калькулятор золотого перетину - тут
Відсотковий калькулятор - тут
Останнє і є золотий розподіл або розподіл відрізка в крайньому і середньому відношенні.
Золотий перетин - це таке пропорційне ділення відрізка на нерівні частини, при якому весь відрізок так відноситься до більшої частини, як сама велика частина відноситься до меншої; або іншими словами, менший відрізок так відноситься до більшого, як більший до всього.
a: b = b: c або з: b = b: а.
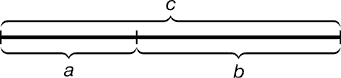
Рис. 1. Геометричне зображення золотої пропорції
Практичне знайомство із золотим перетином починають з розподілу відрізка прямої в золотій пропорції за допомогою циркуля і лінійки.
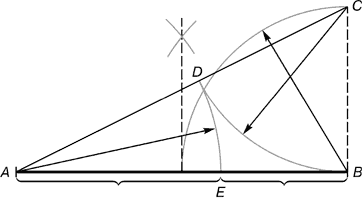
Рис. 2. Розподіл відрізка прямої по золотому перерізу. BC = 1/2 AB; CD = BC
З точки В підіймали перпендикуляр, рівний половині АВ. Отримана точка З з'єднується лінією з точкою А. На отриманій лінії відкладається відрізок ВС, що закінчується точкою D. Відрізок AD переноситься на пряму АВ. Отримана при цьому точка Е ділить відрізок АВ у співвідношенні золотої пропорції.
Відрізки золотий пропорції виражаються нескінченним ірраціональним дробом AE = 0,618 ..., якщо АВ прийняти за одиницю, ВЕ = 0,382 ... Для практичних цілей часто використовують наближені значення 0,62 і 0,38. Якщо відрізок АВ прийняти за 100 частин, то більша частина відрізка дорівнює 62, а менша - 38 частинам.
Властивості золотого перетину описуються рівнянням:
x 2 - x - 1 = 0.
Рішення цього рівняння:

Властивості золотого перетину створили навколо цього числа романтичний ореол таємничості і мало не містичного поклоніння.
В Інтернеті є сервіс який автоматично розраховує золоту пропорцію відрізка:
Другий золотий перетин
Існує і "другий золотий перетин", яке випливає з основного перетину і дає інше співвідношення 44: 56.
Така пропорція виявлена в архітектурі, а також має місце при побудові композицій зображень подовженого горизонтального формату.
|
|
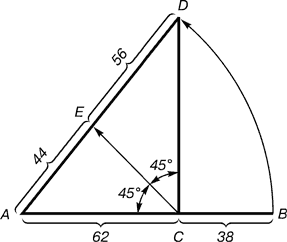
Ділення здійснюється наступним чином. Відрізок АВ ділиться в пропорції золотого перетину. З точки С, підіймали перпендикуляр СD. Радіусом АВ знаходиться точка D, яка з'єднується лінією з точкою А. Прямий кут АСD ділиться навпіл. З точки С проводиться лінія до перетину з лінією AD. Точка Е ділить відрізок AD у відношенні 56: 44. |
Рис. 3. Побудова другого золотого перетину

Рис. 4. Розподіл прямокутника лінією другого золотого перетину
На малюнку показано положення лінії другого золотого перетину. Вона знаходиться посередині між лінією золотого перетину і середньою лінією прямокутника.
Золотий трикутник
Для знаходження відрізків золотої пропорції висхідного і низхідного рядів можна користуватися пентаграмою.

Рис. 5. Побудова правильного п'ятикутника і пентаграми
Для побудови пентаграми необхідно побудувати правильний п'ятикутник. Спосіб його побудови розробив німецький живописець і графік Альбрехт Дюрер (1471 ... 1528). Нехай O - центр кола, A - точка на колі і Е - середина відрізка ОА. Перпендикуляр до радіуса ОА, восставленний в точці О, перетинається з окружністю в точці D. Користуючись циркулем, відкладемо на діаметрі відрізок CE = ED. Довжина сторони вписаного в коло правильного п'ятикутника дорівнює DC. Відкладаємо на колі відрізки DC і отримаємо п'ять точок для накреслення правильного п'ятикутника. З'єднуємо кути п'ятикутника через один діагоналями і отримуємо пентаграму. Всі діагоналі п'ятикутника ділять один одного на відрізки, пов'язані між собою золотою пропорцією.
Кожен кінець п'ятикутною зірки являє собою золотий трикутник. Його сторони утворюють кут 36 ° при вершині, а підстава, відкладене на бічну сторону, ділить її в пропорції золотого перетину.
|
|
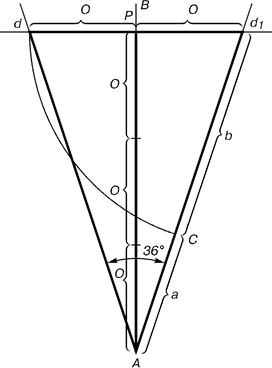
Проводимо пряму АВ. Від точки А відкладаємо на ній три рази відрізок О довільної величини, через отриману точку Р проводимо перпендикуляр до лінії АВ, на перпендикуляре вправо і вліво від точки Р відкладаємо відрізки Про. Отримані точки d і d 1 з'єднуємо прямими з точкою А. Відрізок dd 1 відкладаємо на лінію Ad 1, отримуючи точку С. Вона розділила лінію Ad 1 в пропорції золотого перетину. Лініями Ad 1 і dd 1 користуються для побудови «золотого» прямокутника. |
Рис. 6. Побудова золотого трикутника
Золоті пропорції в частинах тіла людини
У 1855 р. німецький дослідник золотого перетину професор Цейзинг опублікував свою працю «Естетичні дослідження». З Цейзинг відбулося саме те, що й повинно було неминуче відбутися з дослідником, який розглядає явище як таке, без зв'язку з іншими явищами. Він абсолютизував пропорцію золотого перетину, оголосивши її універсальною для всіх явищ природи і мистецтва. У Цейзинга були численні послідовники, але були й противники, які оголосили його вчення про пропорції «математичної естетикою».

Рис. 10. Золоті пропорції в частинах тіла людини
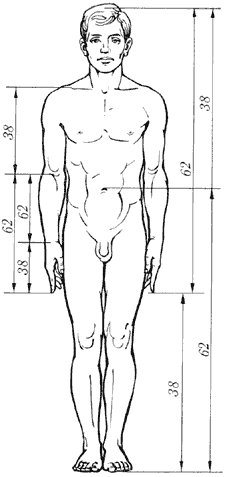
Рис. 11. Золоті пропорції у фігурі людини
Цейзинг виконав колосальну роботу. Він виміряв близько двох тисяч людських тіл і дійшов висновку, що золотий перетин виражає середній статистичний закон. Ділення тіла точкою пупа - найважливіший показник золотого перетину. Пропорції чоловічого тіла коливаються в межах середнього відношення 13: 8 = 1,625 і трохи ближче підходять до золотого перерізу, ніж пропорції жіночого тіла, щодо якого середнє значення пропорції виражається в співвідношенні 8: 5 = 1,6. У новонародженого пропорція становить відношення 1: 1, до 13 років вона дорівнює 1,6, а до 21 року дорівнює чоловічий. Пропорції золотого перетину проявляються і у відношенні інших частин тіла - довжина плеча, передпліччя і кисті, кисті і пальців і т.д.
Справедливість своєї теорії Цейзинг перевіряв на грецьких статуях. Найбільш докладно він розробив пропорції Аполлона Бельведерського. Зазнали дослідженню грецькі вази, архітектурні споруди різних епох, рослини, тварини, пташині яйця, музичні тони, віршовані розміри. Цейзинг дав визначення золотому перетину, показав, як воно виражається у відрізках прямій і в цифрах. Коли цифри, що виражають довжини відрізків, були отримані, Цейзинг побачив, що вони складають ряд Фібоначчі, який можна продовжувати до нескінченності в одну і в іншу сторону. Наступна його книга мала назву «Золоте поділ як основний морфологічний закон у природі та мистецтві». У 1876 р. в Росії була видана невелика книжка, майже брошура, з викладом цієї праці Цейзинга. Автор сховався під ініціалами Ю.Ф.В. У цьому виданні не згадано ні один твір живопису.
У кінці XIX - початку XX ст. з'явилося чимало чисто формалістичних теорії про застосування золотого перетину у творах мистецтва і архітектури. З розвитком дизайну і технічної естетики чинність закону золотого перетину поширилася на конструювання машин, меблів і т.д.
Ряд Фібоначчі
З історією золотого перетину непрямим чином пов'язане ім'я італійського математика ченця Леонардо з Пізи, більш відомого під ім'ям Фібоначчі (син Боначчі). Він багато подорожував по Сходу, познайомив Європу з індійськими (арабськими) цифрами. У 1202 г вийшов у світ його математична праця «Книга про абаці» (лічильної дошці), в якому були зібрані всі відомі на той час завдання. Одне із завдань проголошувала «Скільки пар кроликів в один рік від однієї пари народиться». Розмірковуючи на цю тему, Фібоначчі вибудував такий ряд цифр:
| Місяці | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | і т.д. |
| Пари кроликів | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | і т.д. |
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 і т.д. відомий як ряд Фібоначчі. Особливість послідовності чисел полягає в тому, що кожен її член, починаючи з третього, дорівнює сумі двох попередніх 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 і т.д., а відношення суміжніх чисел ряду наближується до золотого поділу. Так, 21: 34 = 0,617, а 34: 55 = 0,618. Це відношення позначається символом Ф . Тільки це відношення - 0,618: 0,382 - дає безперервне розподіл відрізка прямої в золотій пропорції, збільшення його або зменшення до нескінченності, коли менший відрізок так відноситься до більшого, як більший до всього.
Фібоначчі так само займався вирішенням практичних потреб торгівлі: з допомогою якого найменшої кількості гир можна зважити товар? Фібоначчі доводить, що оптимальною є така система гир: 1, 2, 4, 8, 16 ...
Принципи формоутворення в природі
Все, що набувало якусь форму, утворювалося, росло, прагнуло зайняти місце в просторі і зберегти себе. Це прагнення знаходить здійснення в основному в двох варіантах - зростання вгору або розстеляння по поверхні землі і закручування по спіралі.
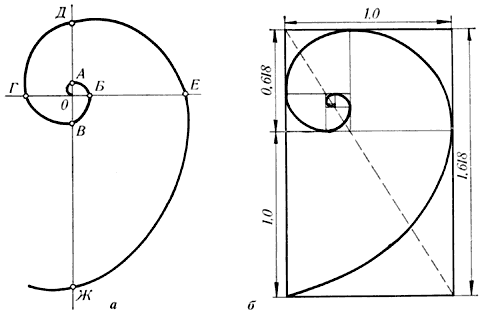
Рис. 12. Спіраль Архімеда
Форма спірально завитий раковини привернула увагу Архімеда. Він вивчав її і вивів рівняння спіралі. Спіраль, накреслені по цьому рівнянню, називається його ім'ям. Збільшення її кроку завжди рівномірно. В даний час спіраль Архімеда широко застосовується в техніці.
Спіраль Архімеда — крива, яку описує точка M під час її рівномірного руху зі швидкістю v уздовж прямої, що рівномірно обертається в площині навколо однієї зі своїх точок О із кутовою швидкістю ω. Спіраль названо ім'ям Архімеда, який вивчив її властивості. Якщо в початковий момент руху точки М і О збігаються, а полярна вісь збігається з початковим розташуванням рухомої прямої, то рівняння спіралі Архімеда у полярних координатах має вигляд: ρ = аω.

Три повороти на 360° руки спіралі Архімеда
Ще Гете підкреслював тенденцію природи до спіральності. Гвинтоподібне і спиралевидне розташування листя на гілках дерев помітили давно. Спіраль побачили в розташуванні насіння соняшнику, в шишках сосни, ананасах, кактуси і т.д. Спільна робота ботаніків і математиків пролила світло на ці дивовижні явища природи. З'ясувалося, що в розташуванні листя на гілці (філотаксіс), насіння соняшнику, шишок сосни проявляє себе ряд Фібоначчі, а стало бути, проявляє себе закон золотого перетину. Павук плете павутину спиралеобразно. Спіраллю закручується ураган. Перелякане стадо північних оленів розбігається по спіралі. Молекула ДНК закручена подвійною спіраллю. Гете називав спіраль "кривою життя».
Серед придорожніх трав росте нічим не примітне рослина - цикорій. Придивімося до нього уважно. Від основного стебла утворився відросток. Тут же розташувався перший листок.
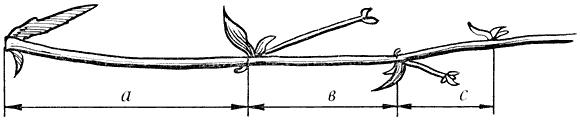
Рис. 13. Цикорій
Відросток робить сильний викид у простір, зупиняється, випускає листок, але вже коротше першого, знову робить викид у простір, але вже меншої сили, випускає листок ще меншого розміру і знову викид. Якщо перший викид прийняти за 100 одиниць, то другий дорівнює 62 одиницям, третій - 38, четвертий - 24 і т.д. Довжина пелюсток теж підпорядкована золотий пропорції. У зростанні, завоюванні простору рослина зберігало певні пропорції. Імпульси його зростання поступово зменшувалися в пропорції золотого перетину.
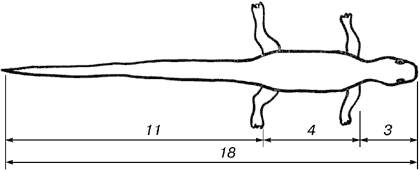
Рис. 14. Ящірка живородяща
У ящірці з першого погляду уловлюються приємні для нашого ока пропорції - довжина її хвоста так відноситься до довжини решти тіла, як 62 до 38.
І в рослинному, і в тваринному світі наполегливо пробивається формотворна тенденція природи - симетрія щодо напрямку росту і руху. Тут золотий перетин проявляється в пропорціях частин перпендикулярно до напрямку зростання.
Природа здійснила розподіл на симетричні частини і золоті пропорції. У частинах проявляється повторення будови цілого.

Рис. 15. Яйце птиці
Великий Гете, поет, натураліст і художник (він малював і писав аквареллю), мріяв про створення єдиного вчення про форму та перетворення органічних тіл. Це він ввів у науковий обіг термін морфологія.
П'єр Кюрі на початку нашого століття сформулював ряд глибоких ідей симетрії. Він стверджував, що не можна розглядати симетрію якого-небудь тіла, не враховуючи симетрію навколишнього середовища.
Закономірності «золотої» симетрії виявляються в енергетичних переходах елементарних частинок, в будові деяких хімічних сполук, в планетарних і космічних системах, в генних структурах живих організмів. Ці закономірності, як зазначено вище, є в будові окремих органів людини і тіла в цілому, а також проявляються в біоритмі і функціонуванні головного мозку і зорового сприйняття.
Джерела інформації:
- Ковальов Ф.В. Золотий перетин в живописі. К.: Вища школа, 1989.
- Кеплер І. Про шестикутних сніжинка. - М., 1982.
- Дюрер А. Щоденники, листи, трактати - Л., М., 1957.
- Стахов А. Коди золотої пропорції.